在讲解本节内容之前,我们先来回顾栈和队列的特点。
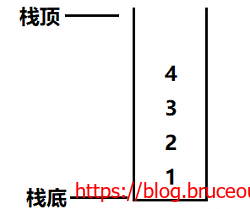
栈的特点是先进后出,例如,把序列1,2,3,4,存入栈中。
入栈:1先入,4最后入,最终1在栈底,而4位于栈顶。
出栈:栈顶先出,最后栈底元素出栈。
==队列的特点==是先进先出,例如,把序列1,2,3,4,存入队列中。
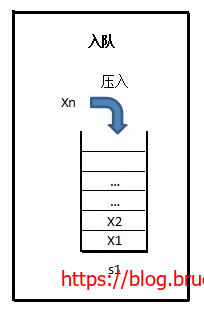
入队:1先入,4最后入,最终1在队首,而4位于队尾。
出队:队首先出,最后队尾元素出队列。

使用两个栈来实现一个队列,其实就是组合两个栈,来实现队列,栈是先进后出,队列是先进先出。好了,下面来看看代码实现。我们主要讲解用栈实现队列的出队和入队。
6.1入队
入队就比较简单,把需要存放的元素插入到栈1中即可,此时栈2为空。
int Sequeue_En(seqstack_t *stack1,int k)
{
if(stack1 == NULL)
{
return -1;
}
PushStack(stack1, k);
return 0;
}6.2出队
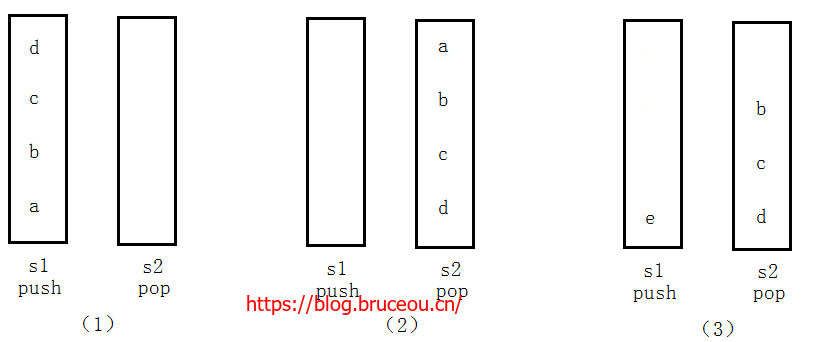
首先将栈stack1中的元素出栈再将其元素入栈stack2中,此时出栈stack2中的元素,就可以达到和队列删除数据一样的顺序了。
data_t Dequeue_De(seqstack_t *stack1,seqstack_t *stack2,int *x)
{
if(stack1 == NULL || stack2 == NULL)
{
return -1;
}
else
{
if(EmptyStack(stack1) && EmptyStack(stack2))
{
printf("This queue is empty\n");
}
if(EmptyStack(stack2) == 0)
{
PopStack(stack2,x);
}
else
{
while(EmptyStack(stack1) == 0)
{
PopStack(stack1,x);
if(FullStack(stack2))
{
printf("stack full!\n");
}
else
{
PushStack(stack2,*x);
}
}
PopStack(stack2,x);
}
}
return 0;
}再上述代码中,还有几处疑惑需要进行解答,当2只pop了一个元素a时,1中可能还会插入元素e,这时如果将s1中的元素e插入s2中,在a之后出栈的元素就是e了,显然,这样想是不对的,我们必须规定当s2中的元素pop完之后,也就是s2为空时,再插入s1中的元素。
资源获取方法
1.关注公众号[嵌入式实验楼]
2.在公众号回复关键词[Data Structures and Algorithms]获取资料提取码


